This Technical Brief provides a general overview of the concept of the zeta potential (ZP). We will discuss the two parameters that control the nature and behavior of every system in which one phase is dispersed in another phase. In a system, the first phase is called the disperse phase, or the phase forming the particles, and the second is the dispersion medium, or the fluid in which the particles are distributed. The two parameters we will focus on are the extent of the interface and the interfacial chemistry of the disperse phase. The physicomechanical and physicochemical characteristics that constitute the two respective fundamental parameters are summarized in Table 1. The interfacial chemistry is often a neglected parameter in pharmaceutical applications even though, in some applications, it is as or more important than the interfacial extent.

The physical nature of any dispersion depends on the respective roles of the constituent phases. There are numerous examples of dispersed systems, including foams (gas-in-liquid), emulsions (liquid-in-liquid), and aerosols (solid-in-gas or liquid-in-gas), that have found application in pharmaceuticals. We will focus on the most widely-formulated type of dispersion, which is suspensions (solid-in-liquid).

The ZP (symbol ζ) is related to the surface charge, a property that all materials possess, or acquire, when suspended in a fluid. The sign and magnitude of ZP affects process control, quality control, and product specification. At the simplest level, it can help maintain a more consistent product and at a complex level, it can improve product quality and performance. At the very least its measurement answers the question: Is the electrical charge on the material particle positive or negative? This information is often sufficient to guide formulation or processing. The next higher level of inquiry has to do with quality control: Has the product sufficient electrostatic repulsion to maintain its stability?

The Origin of Charge in Polar Media

All materials will spontaneously acquire a surface electrical charge when brought into contact with a polar medium (i.e., water)¹. Generally, an interface in deionized water is negatively charged, but there are materials that can be positive². The various charging mechanisms are found below and will be considered in turn:

• Electron affinity differences of two phases
• Ionization of surface groups
• Differential ion adsorption from electrolyte solution
• Differential ion dissolution from a crystal lattice
• Surface anisotropy
• Isomorphous substitution

Electron affinity differences of two phases is responsible for the development of the contact potential between dissimilar metals and is important in corrosion and thermoelectric effects³. This mechanism is a dominant process in initially determining the surface charge at the metal-solution interface. Nanoparticulate metal solutions are being studied in a wide variety of applications because they offer greatly enhanced performance. Their inherent surface charge is critical to any further processing or use. 

Ionization of surface groups is observed with all metal oxide surfaces (M-OH), as well as materials that contain carboxyl and/or amino groups. This latter category includes proteins, ionic polymers, and poly-electrolytes, many of which are widely utilized in pharmaceutical formulations. The ionization and/or dissociation of these groups (degree of charge development) and the net molecular charge (and thus sign, either positive or negative) depends strongly on the pH of the dispersion media.

In differential ion adsorption from electrolyte solution, a net surface charge arises through the process of unequal adsorption of oppositely charged ions and may result in either a net positive or net negative surface. Many lyophobic material suspensions (i.e., polymer latexes and active pharmaceutical ingredients (APIs)) fall into this category. If surfactant ions are present, their adsorption will tend to determine the net surface charge.

Ionic solids, such as calcite (CaCO3), hydroxyapatite [Ca5(PO4)3(OH)], and barite (BaSO4), can acquire a surface charge via differential ion dissolution from a crystal lattice by unequal dissolution of the oppositely charged ions. Addition of small concentrations of Ca²⁺ ions (10^-3 M) by using CaCl₂, for example, can adjust the net charge of a suspension of CaCO₃; the hardness of water becomes a factor that must be considered.

Surface anisotropy are defects in a crystal lattice that result in the development of negative and positive charges. For mineral oxides, this results in amphoteric hydroxyl groups that can undergo a reaction with either H⁺ or OH-. One pharmaceutically useful material in this group is the silicas⁴; the surface charge is negative because the silanol groups (-SiOH) are weakly acidic.

The oxides of most divalent and trivalent metals (e.g., MgO and Al₂O₃, respectively) are amphoteric; any dissolution tends to be in the form of the hydroxide. Swings in solution pH must be avoided because it can cause re-precipitation back onto the oxide surface in a different chemical form thus altering the surface chemistry and hence charge.

Isomorphous substitution is a more extreme case of Isomorphous substitution. It occurs in clay materials (i.e., montmorillonite and vermiculite), where a large negative charge arises because of the difference in valence between the Al³⁺ and the Si⁴⁺ ions in the alumino-silicate crystal structure⁵; varying proportions of minor elements leads to a dizzying variety and complexity of minerals⁶. The net surface charge of any clay depends on the clay’s pre-history and as such it may not be possible to substitute clay from a given manufacturer with that from another.

Electrical Properties in Non-aqueous Media

In solvents with moderate dielectric constants (>10 compared with ~80 for water), some degree of ionization is possible; charging mechanisms parallel to those in water can occur. Examples include low molecular weight alcohols, amines, aldehydes, and ketones; ionic surfactants (ex. Aerosol OT) and some simple ionic salts (ex. LiCl) can dissociate to some extent in such media.

Although electrolytes cannot ionize in fully nonpolar media (solvents of very low dielectric constants, ~2, such as alkanes), particles dispersed in such a medium can acquire charge. Electrostatic forces are important and play a key role in stabilizing non-aqueous suspensions, but the charging mechanism is not the same as in aqueous dispersions⁷. These charges arise because of acid-base (or electron donor-acceptor) interactions between the particle surface and the dispersing agent⁸ which is why acidic (ie. polyvinylchloride) or basic (ex.  polymethylmethacrylate) polymers are very effective suspenders of particles in non-aqueous media.

The Electric Double-Layer

A particle dispersed in a liquid is solvated and the extent of the solvated layer is influenced by the solution conditions such as composition (ex. pH, ionic strength), temperature, and pressure⁹. The boundary between the edge of this solvated layer and bulk liquid is termed the shear plane.

Regardless of how charge separation is generated, the distribution of electrical charges at the interface is different from that in the bulk liquid phase. A “structure”, called the electric double-layer (EDL) will be developed such that the particle surface charge is neutralized by an adjacent layer in solution containing an excess of ions of opposite charge to that of the surface, i.e., counterions; ions of the same charge as the surface are termed co-ions. The theory of the electric double-layer, (EDL) is extremely complex and mostly beyond the scope of this overview, but we will briefly touch upon some concepts¹⁰.

The EDL can be regarded as consisting of two regions or layers (hence the term electric double-layer; Figure 2): a region closest to the surface, called the Stern layer, that is considered immobile and may include adsorbed ions, and an outer region, called the diffuse layer, that allows diffusion of ions distributed according to the influence of electrical forces and random thermal motion.

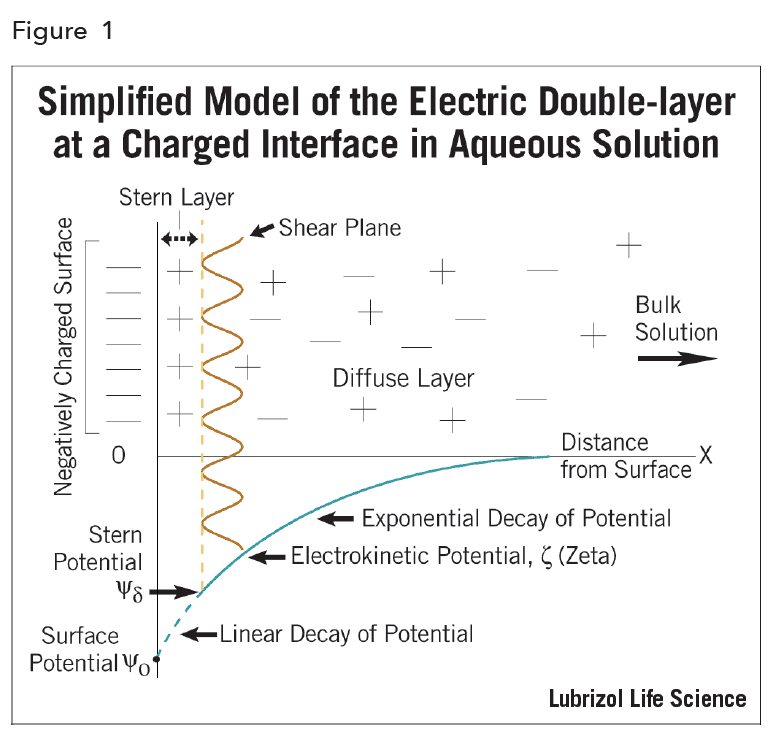The electric potential decreases linearly from Ψ_o, the actual thermodynamic surface potential, to the Stern potential, Ψd and then it decays exponentially to zero in the diffuse layer. This is described by:

Ψ = Ψd exp [- κX]

where, x is the distance from the material surface and κ, called the Debye-Hückel parameter, is defined as:

κ = [2e²N_Acz²/єє_okbT]^½

where, e is the protonic charge, NA is Avogadro’s constant, c is the concentration of electrolyte of valence, z, є is the dielectric constant, є_o, is the permittivity of free space, and kb is the Boltzmann constant.

Hence, it can be seen that the electric potential depends (through κ) on the ionic composition of the medium. If κ is increased, and the electric double layer is “compressed”, then the potential must decrease.

Unfortunately, the fundamental interfacial property (Ψo) is inaccessible¹¹. What can be derived and measured is an electrokinetic potential – termed the zeta potential ζ. This quantity, defined as the potential at the shear plane, has become a very useful experimental parameter to monitor electrokinetic behavior of suspensions, especially changes in such behavior².

The Relation between Zeta Potential and Surface Charge

Although ζ is not the actual thermodynamic (or surface) potential, in theoretical calculations, ζ is frequently taken to be identical with the Stern potential, Ψ_d.

When specific adsorption of charged moieties occurs at a surface, counterion adsorption usually predominates over co-ion adsorption. With polyvalent and surface-active counterions, it is possible for a reversal of charge to take place within the Stern player – i.e., for Ψ_o and Ψ_d (and, hence ζ) to have opposite signs.

The adsorption of nonionic (i.e., polyoxyethylene-based) surfactants would result in a ζ being close to zero. As the molecular weight of any macromolecular species increases, it results in the shear plane being located at a larger distance from the Stern plane. All these types of “charge modifying agents” are used extensively in the formulation of suspensions.

Thus, it is possible that a surface can have an inherent (thermodynamic) charge, but have no measurable ZP and vice-versa¹². This does not imply that the ZP measurement is not useful.  On the contrary, ζ is, in the practical sense, the effectiveness of the particle surface charge in solution. While ζ may derive initially from the fundamental number of surface sites, (how many, what type, etc.), more important are the solution conditions themselves because they control the resulting final sign and magnitude of ζ. The consequence of this to the process of dispersing particles is critical. And importantly, it is useless to quote a measured ζ value without specifying the suspension conditions under which the measurement was made.

References

1. Lyklema J, Fundamentals of Interface and Colloid Science. Amsterdam, The Netherlands: Elsevier Publishing Company (1991).
2. Hunter RJ, Zeta Potential in Colloid Science. London, England: Academic Press (1981)
3. Fisher LH and Varney RN, Am. Journal of Physics,44(5): 464- 475 (1976).
4. Iler RK, Chemistry of Silica. Weinheim, Germany: Wiley-VCH Verlag (1979).
5. van Olphen H, Introduction to Clay Colloid Chemistry. London, England: Interscience Publishers (1963).
6. Carmichael RS, Physical Properties of Rocks and Minerals. Boca Raton, FL, USA: CRC Press Inc. (1989).
7. Pugh RJ et al, Colloids and Surfaces, 7: 183-287 (1983).
8. Fowkes FM et al, in Nonaqueous Liquids. ACS Symposium Series, No.200. Chapter 11: 307-324 (1982).
9. Hunter RJ, Foundations of Colloid Science. 2nd Edition. Oxford, England: Oxford University Press (2001).
10. Parsons R, J. Electroanalytical and Interfacial Electrochemistry, 118(2): 3-18 (1981).
11. Guggenheim EA, J. Phys. Chem., 33: 842-849 (1929).
12. Miller NP and Berg JC, Colloids and Surfaces, 59:119-128 (1991).